Kì thi vào lớp 10 được xem là bước ngoặt lớn thứ nhất trên chặng đường học tập của các em. Ở tiến trình này, tâm lý của những em khá lo lắng do lượng loài kiến thức rất nhiều và sách tìm hiểu thêm thì đa dạng, học tập sách nào bắt đầu đúngtrọng tâm. Dưới đây, Newshop hỗ trợ các em tổng hợp các kiến thức trọng tâm môn toán và một số cuốn sách ôn thi vào lớp 10 môn toán tốt được nhiều người học sinh và thầy cô chọn lựa làm tài liệu tham khảo, ship hàng cho quy trình dạy cùng học.
Bạn đang xem: Luyện thi lớp 10 môn toán

CHUYÊN ĐỀ 1: RÚT GỌN VÀ TÍNH GIÁ TRỊ CỦA BIỂU THỨC




CHUYÊN ĐỀ 2: GIẢI PHƯƠNG TRÌNH VÀ HỆ PHƯƠNG TRÌNH BẬC NHẤT nhì ẨN







CHUYÊN ĐỀ 3: PHƯƠNG TRÌNH BẬC nhị MỘT ẨN




CHUYÊN ĐỀ 4: GIẢI BÀI TOÁN BẰNG CÁCH LẬP PHƯƠNG TÌNH VÀ HỆ PHƯƠNG TRÌNH




GỢI Ý CÁC BỘSÁCH ÔN THI VÀO LỚP 10 MÔN TOÁN CỰC HAY mang đến HỌC SINH
CỦNG CỐ KIẾN THỨC ÔN THI VÀO LỚP 10 thpt - MÔN TOÁN
Kỳ thivào lớp 10đang ngày 1 đến ngay gần hơn. Vì đó,việcchuẩn bị đồ vật kiến thức, năng lực vàtâm líổn định là vô cùng đặc trưng với các bạn học sinh để quy trình ôn tập và tiến hành bài thi đạt tác dụng tốt nhất.
Với sứ mệnh hỗ trợ vàđồng hành với những bạnhọc sinh trong quá trình ônvào lớp 10 THPT.Củng Cố kỹ năng Ôn Thi Vào Lớp 10 THPTvới 2 môn thi chính là Toán, Ngữ Văn, giờ đồng hồ Anh đã có được cho soạn và đã tạo ra đời.Hầu hết văn bản củamỗi đầusách được tạo ra đều bám sát đít vào chuẩn chỉnh kiến vật dụng cũng nhưkĩ năng trường đoản cú khungchương trình giáo dục THCS bây chừ dựatheo nấc độ reviews năng lực học sinh cùngyêu cầu cho các phương ántổ chức đến kỳthi vào lớp 10 của sở GD & ĐT. Kỹ năng vàđề thi ôn tập cho các môn thi được phân loại đầy đủtheo các mức độ:Nhận biết, thông hiểu, áp dụng thấp và vận dụng cao.Với môn Toán, cấu trúc sách bao hàm ba phần chính:+ Tổng hòa hợp và khối hệ thống hóa những kiến thức theo chương trình chính thức.+ một số trong những đề thi xem thêm hayđược xây dựng sáttheo cấu trúc đề thi vào lớp 10 thpt được đưa ra.+ Phụ lục chú giải tựamột số đề thi bao gồm thức.

BỒI DƯỠNG HỌC SINH GIỎI trung học cơ sở VÀ ÔN LUYỆN THI VÀO LỚP 10 thpt CHUYÊN MÔN TOÁN
Đầu sách được biên soạn nhằm giúp chúng ta học sinh đạt được nguồn tư liệu ôn tập, góp củng cố kiến thức thật vững vàng vàng cho các kỳ thi học tập sinh giỏi Toán THCS cũng tương tự ôn thi vào các trường thpt và trung học phổ thông Chuyên. Câu chữ được phân chia qua nhì phần chính:
Phần 1: tập hợp14 siêng đề hệ thống phần lớn cácnội dung cơ bản của môn Toán thuộc chương thcs cũng nhưcác vấn đề trọng yếu cho việc ôn thi. Ở mỗi chuyên đề, tác giả đều kể lại những khái niệm cũng như cáckiến thức cơ bạn dạng mà các bạnhọc sinh đề xuất nắm. Hơn hết, cuối mỗi siêng đề còn đựng đựng những mẫu bài tập góp các bạn cũng có thể chủ hễ tăng cườngrèn luyện tài năng tư duy toán học. Đồng thời, sách cònkèm theo phần lí giải giải đề nhằm mục đích giúp các bạnhọc sinh có thể so sánh vàđối chiếu với bí quyết giải của mình.
Phần 2: mộtsố đề thi vàocác trường trung học phổ thông vàTHPT chuyên được tinh lọc quanhững năm sát đây.
Kỳ thi tuyển thi vào lớp 10 sắp tới ngày một ngay sát hơn. Đây cũng chính là khoảng thời hạn mà chúng ta học sinh đề xuất tập trung đa số thời gian vào hoạt động ôn thi để nâng cấp điểm số. Cùng với môn Toán, một trong những những môn thi bắt buộc, baivanmau.edu.vn sẽ giới thiệu một vài nhắc nhở về cách thức ôn thi vào lớp 10 cho hầu hết ai còn băn khoăn về cách học và luyện thi.
Phương pháp ôn thi Toán vào 10
Để quá trình ôn luyện trở nên tác dụng hơn, các bạn học sinh nên có phương thức ôn thi hợp lý và phải chăng nhất. Sau đó là những lời khuyên của giáo viên Hồng Trí quang quẻ – thầy giáo môn Toán tại khối hệ thống Giáo dục baivanmau.edu.vn ao ước gửi đến chúng ta học sinh giữa những ngày thi cận kề này
Tập trung ôn phần kiến thức trọng tâm
Phần kỹ năng trọng trọng điểm là những kỹ năng và kiến thức có trong kết cấu đề thi. Những thắc mắc cơ bạn dạng từ câu 1 mang lại câu 3 phải đảm bảo nhuần nhuyễn, hoàn toàn có thể vận dụng linh hoạt kim chỉ nan đã được học, tránh đều lỗi sai nhỏ dại nhặt dẫn mang lại trừ điểm đáng tiếc trong bài bác thi.
Đối với những câu hỏi có chứa áp dụng cao như câu 4 với câu 5, các bạn học sinh nên dành nhiều thời gian để ôn tập hơn, không nên quá ép bạn dạng thân đề xuất làm hết các phần ngoài năng lực của mình. Tập trung làm thật chậm rãi và chắc các phần nằm trong khả năng của bản thân mình là quan trọng nhất.
Có kim chỉ nam và lộ trình rõ ràng
Ôn thi vào 10 là một hành trình dài với cần tương đối nhiều sự nỗ lực và cố gắng tự học tập từ các bạn học sinh. Theo đó, chúng ta nên lập ra chiến lược và tất cả mục tiêu cụ thể cho từng giai đoạn, ví dụ như như tiến trình ôn tập, quy trình tiến độ luyện đề, giai đoạn cải thiện điểm.
Trong quy trình luyện đề, các bạn học sinh cũng cần để ý lựa lựa chọn tài liệu phù hợp, update với xu hướng ra đề năm nay. Tài liệu nên bao gồm kèm lời giải, giải đáp để dễ dàng đối chiếu, kiểm soát và điều chỉnh cách làm thế nào cho đúng, cung cấp cho quá trình tự học trở nên kết quả hơn.

Kiến thức giữa trung tâm ôn thi vào lớp 10 môn Toán
Về kiến thức và kỹ năng trọng tâm bao gồm ổng cùng 16 chuyên đề chủ yếu trải hầu như trong 2 phần đại số và hình học. Cùng với những kỹ năng và kiến thức này, những em học sinh không chỉ việc nắm vững vàng lý thuyết, các kiến thức tương quan mà còn nên dành thời gian cho việc thực hành thực tế trực tiếp trên bài tập hoặc bên trên đề thi các năm. Điều này không những giúp những em cố chắc kỹ năng một cách xúc tích và ngắn gọn mà còn luyện tập thói quyen tương tự như phản xạ làm bài xích một biện pháp nhanh chóng, máu kiệm thời hạn trong quy trình làm bài xích thi.
Các kiến thức trọng trọng điểm ôn thi tốt nghiệp lớp 10 môn Toán bao gồm có:
Phần I: siêng đề Đại số
Rút gọn với tính giá trị biểu thứcGiải phương trình cùng hệ phương trình số 1 2 ẩn
Phương trình bậc 2 một ẩn
Giải toán bằng cách lập phương trình hoặc hệ phương trình
Hàm số và đồ thị
Chứng minh bất đẳng thức
Giải bất phương trình
Tìm giá trị to nhất, nhỏ nhất của biểu thức
Giải việc có nội dung số học
Phần II: chuyên đề hình học
Chứng minh những hệ thức hình họcChứng minh tứ giác nội tiếp và nhiều điểm thuộc nằm trê tuyến phố tròn
Chứng mình dục tình tiếp xúc giữa đường thẳng và mặt đường tròn hoặc 2 đường tròn
Chứng minh những điểm nỗ lực định: khẳng định bao nhiều loại yếu tố
Bài tập hình gồm nội dung tính toán
Quỹ tích cùng dựng hình
Bài toán về rất trị hình học
Phần II: chăm đề Hình học
Phần III: Đề thi tham khảo
Phần IV: giải mã và đáp số
Nắm trọn con kiến thức các môn ôn thi vào 10 đạt 9+ với bộ sách

Các dạng bài giữa trung tâm thường gặp gỡ ôn thi vào lớp 10 môn Toán
Dạng I: Rút gọn gàng biểu thức gồm chứa căn thức bậc hai
Trong các dạng toán thi vào lớp 10, đấy là dạng toán cơ phiên bản các em học sinh đã được học trong lịch trình Toán lớp 9. Đề có tác dụng được dạng này đòi hỏiu các em đề nghị nắm vững chắc định nghĩa căn bậc nhì số học tập và những quy tắc để thay đổi căn bậc hai. Để thuận tiện cho việc ôn tập, baivanmau.edu.vn chia dạng này thành 2 loại bao gồm: biểu thức số học với biểu thức đại số.
1/ Biểu thức số học
Phương pháp làm bài:
Sử dụng những công thức đổi khác căn thức được học: đưa ra phân tích ; đưa vào ;khử căn thức; trục căn thức; cộng, trừ hồ hết căn thức đồng dạng; rút gọn gàng phân số…) để rút gọn gàng biểu thức một phương pháp ngắn nhất.
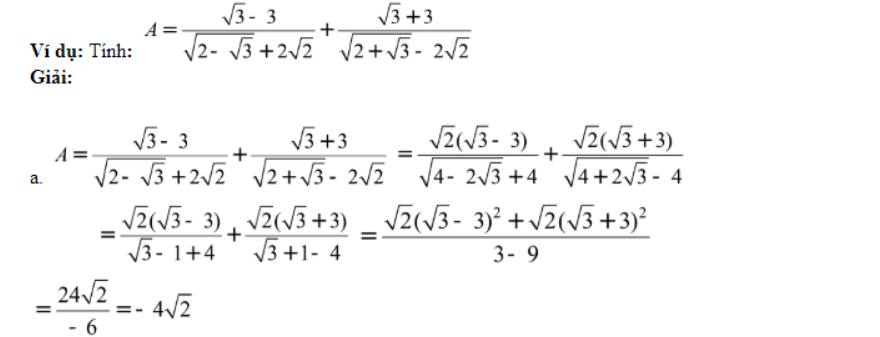
2/ Biểu thức đại số:
Phương pháp làm bài:
– Phân tích nhiều thức phân số với tử và chủng loại thành nhân tử;– kiếm tìm điều kiện khẳng định đa thức– thực hiện rút gọn gàng từng phân thức– Sử dụng những phương pháp đổi khác đồng tốt nhất như:+ Quy đồng (sử dụng trong các dạng bài cộng trừ) ; nhân ,chia.+ vứt ngoặc đơn, ngoặc kép: bằng phương pháp nhân solo hay đa thức hoặc thực hiện hằng đẳng thức đáng nhớ+ Thu gọn: cộng, trừ các hạng tử đồng dạng.+ Sử dụng phương thức phân tích đa thức thành nhân tử

Dạng II: Đồ thị y = ax + b (a ≠ 0) và y = ax2 (a ≠ 0), đối sánh giữa chúng
Trong các dạng vào đề thi toán vào lớp 10, để làm các dạng toán có tương quan tới đồ dùng thị hàm số em học sinh bắt buộc phải nắm được khái niệm và hình thái của các dạng trang bị thị hàm hàng đầu (dạng con đường thẳng), hàm bậc nhì (parabol), hàm bậc 3 (dấu ngã) hay những dạng đồ dùng thị đối xứng. Một trong những dạng bài xích về đồ dùng thị bao gồm có:
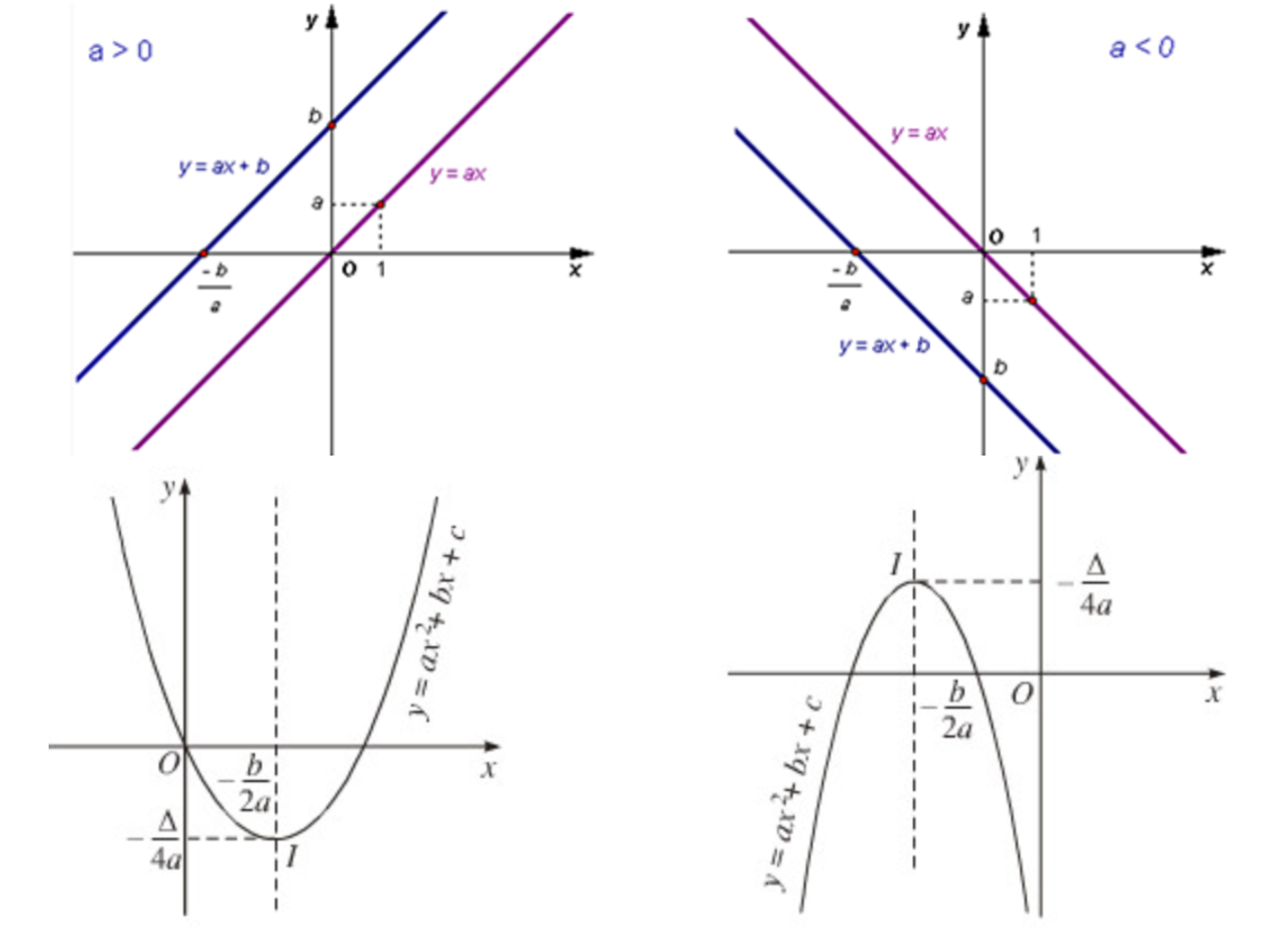
1. Điểm thuộc con đường – đường đi qua điểm.
Phương pháp giải bài bác tập: Điểm A(x
A; y
A) thuộc đồ gia dụng thị hàm số y = f(x) y
A = f(x
A).
VD: Tìm thông số a của hàm số: y = ax2 biết đồ vật thị hàm số của nó đi qua điểm A(2;4)
Giải:
Do đồ thị hàm số trải qua điểm A(2;4) nên: 4 = a.22 ⇔ a = 1
2. Cách tìm giao điểm của hai tuyến đường y = f(x) cùng y = g(x).
Phương pháp giải bài bác tập: để triển khai được dạng bài này, những em học viên thực hiện tại theo các bước sau:
Bước 1: tìm hoành độ giao điểm: đấy là nghiệm của phương trình f(x) = g(x) (*)
Bước 2: áp dụng x đã tìm kiếm được tìm được thế vào một trong những hai bí quyết y = f(x) hoặc y = g(x) để tìm tung độ giao nhau của 2 đồ gia dụng thị con đường thẳng
Lưu ý: Số nghiệm của phương trình (*) sẽ lập nghỉ ngơi trên đó là số giao điểm thân 2 con đường thẳng y = f(x) với y = g(x)
3. Dạng bài xích tìm mối quan hệ giữa (d): y = ax + b với (P): y = a’x² (a’0).
3.1. Tìm kiếm tọa độ giao điểm của (d) với (P).
Phương pháp có tác dụng bài:
Bước 1: tra cứu hoành độ giao điểm là nghiệm của pt:
a’x² = ax + b (#) ⇔ a’x² – ax – b = 0 (1)
Bước 2: áp dụng nghiệm vẫn tìm núm vào hàm số y = ax +b hoặc y = ax² để xác minh tung độ y của giao điểm.
Xem thêm: Giá vốn để làm 1 chiếc đồng hồ tissot fake loại 1 mà bạn cần biết
Lưu ý: Số nghiệm của pt (1) đã tạo ở trên đó là số giao điểm của 2 đường thẳng (d) và (P).
3.2. Tìm điều kiện để (d) cùng (P) cắt; tiếp xúc; không cắt nhau:
Phương pháp có tác dụng bài:
Từ phương trình (#) ta xét các điều kiện nhằm phương trình: ax² – ax – b = 0 có nghiệm, vô nghiệm. Xét Δ = (-a)² + 4ab
a) nếu như phương trình (d) với (P) cắt nhau ⇔ pt gồm hai nghiệm biệt lập ⇔ Δ > 0b) trường hợp phương trình (d) cùng (P) tiếp xúc với nhau ⇔ pt gồm nghiệm kép ⇔ Δ = 0c) trường hợp 2 phương trình (d) và (P) ko giao nhau ⇔ pt vô nghiệm ⇔ Δ Nắm trọn đầy đủ dạng đề thi vào 10 với khóa đào tạo HM10 Luyện đề

Dạng III: Hệ phương trình với phương trình
Giải hệ phương trình với phương trình là trong số những dạng toán cơ phiên bản nhất trong những dạng bài mở ra trong đề thi vào lớp 10 môn Toán. Giải hệ phương trình thực hiện 2 phương pháp là cộng đại số hoặc thế, giải pt bậc nhì ta thực hiện công thức nghiệm. Kề bên đó, baivanmau.edu.vn sẽ giới thiệu thêm một số dạng bài xích chứa tham số liên quan đến phương trình.
1. Hệ phương trình bậc nhất 2 ẩn
Phương pháp giải bài:
+ Dạng tổng quát:
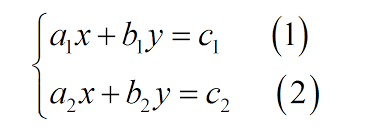
+ bí quyết giải: Để giải phương trình bậc nhất, ta đa số sử dụng 2 phương pháp chủ yếu hèn là
Phương pháp thế.Phương pháp cộng đại số.2. PT bậc nhị + Hệ thức Vi-ét
2.1. Giải pháp giải pt bậc hai có dạng: ax² + bx + c = 0 ( a ≠ 0)
Phương pháp làm bài:

2.2. Định lý Vi-ét:
Phương pháp làm những dạng bài tương quan tới định lý Vi-ét: Áp dụng các hệ trái sau
Nếu x1 với x2 là nghiệm của pt : ax² + bx + c = 0 (a ≠0) thì:
S = x1 + x2 = -b/ap = x1x2 =c/a.Và ngược lại: Nếu có hai số x1, x2 thỏa mãn điều kiện x1 + x2 = S và x1x2 = p. Thì nhì số trên là nghiệm (nếu có) của pt bậc 2 có dạng: x² – Sx + p = 0
3. Tính giá bán trị của các biểu thức nghiệm:
Phương pháp có tác dụng bài: chuyển đổi biểu thức đề bài ra để xuất hiện thêm các biểu thức gồm dạng: (x1+x2) với x1x2
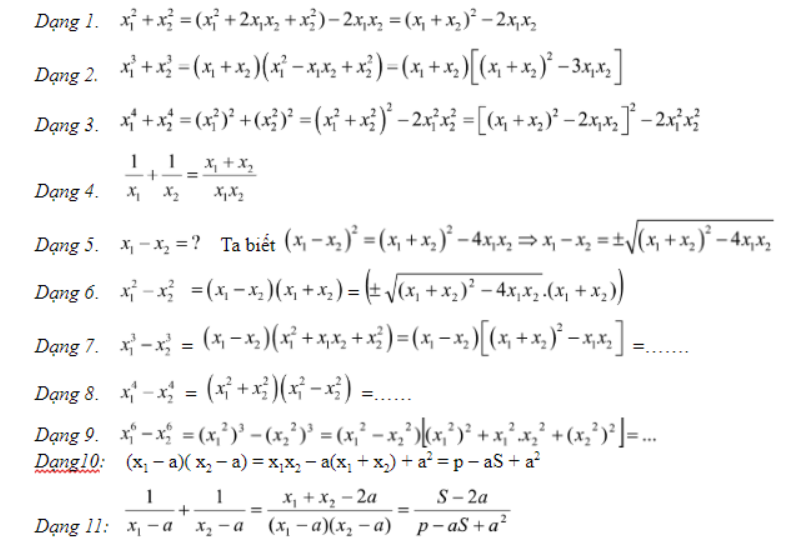
4. Tra cứu hệ thức contact giữa nhị nghiệm của phương trình làm thế nào để cho nó không phụ thuộc vào vào tham số
Phương pháp làm bài:
Bước 1: Tìm đk phương trình đang cho tất cả hai nghiệm x1 cùng x2
(thường là a ≠ 0 với Δ ≥ 0)
Bước 2: Áp dụng hệ thức Vi-ét
Bước 3: phụ thuộc hệ thức Vi-ét để rút biểu thức thành dạng tổng nghiệm hoặc tích nghiệm rồi sau đó đồng điệu các vế với nhau.
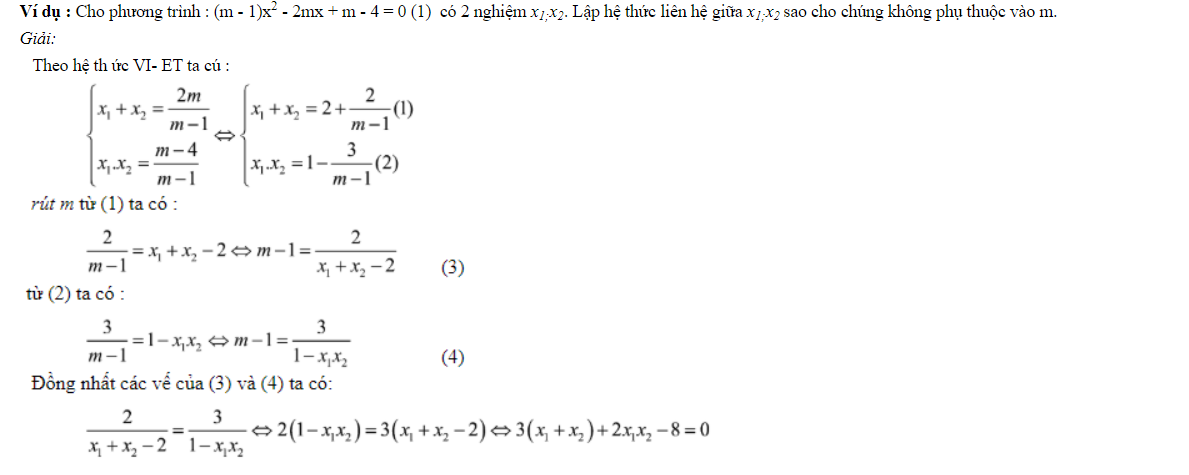
5. Tìm quý hiếm tham số của phương trình thỏa mãn nhu cầu biểu thức đựng nghiệm đã cho
Phương pháp giải bài bác tập:
– Tìm điều kiện để pt có hai nghiệm x1 với x2 (Điều kiện hay là a ≠ 0 với Δ ≥ 0)
– trường đoản cú biểu thức vẫn có, vận dụng hệ thức Vi-ét để giải phương trình
– Đối chiếu với tập xác định của điều kiện của tham số vẫn tìm trước đó nhằm tìm ra đáp án.
Ví dụ minh họa:
Bài 1: cho phương trình có dạng: x2 – 2(m + 3)x + m2 + 3 = 0
a) Giải pt khi m = -1 và m = 3b) search m nhằm phương trình gồm một nghiệm x = 4c) kiếm tìm m để phương trình bao gồm hai nghiệm riêng biệt với nhaud) tìm kiếm m để phương trình gồm hai nghiệm thoả mãn điều kiện x1 = x2
Bài 2: Cho phương trình có dạng : ( m + 1) x2 + 4mx + 4m – 1 = 0
a) Giải phương trình lúc m = -2b) kiếm tìm m để phương trình có hai nghiệm phân biệtc) kiếm tìm m nhằm phương trình tất cả hai nghiệm thoã mãn đk x1 = 2x2
Dạng IV: Giải bài xích toán bằng cách lập phương trình ôn thi tuyển chọn sinh vào lớp 10 môn Toán
Trong các dạng bài lộ diện trong đề thi toán vào lớp 10, đó là một trong những dạng toán rất được yêu thích trong thời gian vừa mới đây vì dạng bài xích này có thể ứng dụng thực tế. Điều này đòi hỏi các em học tập sinh cần phải biết suy luận từ thực tế để đưa vào bí quyết toán.
Phương pháp giải bài tập dạng này:
Bước 1: Lập hệ phương trình hoặc phương trình dựa trên những dữ kiện gồm sẵn đề bài xích ra
Chọn ẩn, đơn vị chức năng của ẩn, các điều kiện với tập xác định của ẩn đang đặt.Biểu đạt các đại lượng và dữ kiện khác dựa vào ẩn (lưu ý đề nghị phải nhất quán đơn vị).Dựa vào những dữ kiện, đk của đề bài xích đã ra để tạo thành phương trình hoặc hệ phương trình.Bước 2: triển khai giải hệ phương trình hoặc hệ phương trình đã sản xuất lập từ cách 1
Bước 3: Kết phù hợp với điều khiếu nại hoặc tập xác định để lấy ra kết luận về nghiệm
Các bí quyết cơ bạn dạng cần nhớ đối trong quá trình giải các bài tập thuộc dạng bài xích vận dụng


Cấu trúc đề thi tuyển chọn sinh vào lớp 10 môn Toán
Nắm chắc cấu tạo của đề thi là cách rất tốt để các bạn học sinh gửi ra giải pháp làm bài bác hợp lí, góp tận dụng tối đa thời gian làm bài thi của mình. Với môn Toán, cấu tạo đề thi qua từng năm không tồn tại quá nhiều biến đổi và sự khác biệt giữa các tỉnh thành cũng không thực sự nhiều. Đề thi thông thường sẽ có 5 câu. Vậy thể:
Cấu trúc cơ bạn dạng của đề thi toán vào lớp 10
Câu 1: Chiếm khoảng 20% tổng điểm. Đây là câu hỏi mang tính kiểm tra kĩ năng thông đọc của học viên về những dạng bài xích thuộc những chuyên đề như:+ biểu thức,+ phương trình,+ bất phương trình,+ tìm cực hiếm x để thỏa mãn yêu cầu,..Lưu ý: Dạng bài bác về bất phương trình cùng tìm cực hiếm x để thỏa mãn đều là đầy đủ dạng bài cải thiện và thường chiếm phần 0,5 điểm.Câu 2: Chiếm khoảng chừng 20% tổng điểm. Hay là những bài toán thực tế, vận dụng kiến thức và kỹ năng về phương trình hoặc hệ phương trình để xử lý bài tập. Câu 2 thường rất có thể sẽ bao gồm 2 yêu cầu nhỏ, vật dụng tự được xếp thứu tự theo độ cực nhọc tăng dần, từ nối liền đến vận dụng.Lưu ý: Trong những năm gần đây, đề bài xích thuộc dạng này thường sẽ có 2 ý chính. Ý thứ nhất thuộc mức độ thông hiểu, bắt buộc những em học viên cần phải nắm vững kiến thức mới có thể giải quyết được. Ý sản phẩm hai nằm trong vòng độ áp dụng thấp, không thực sự khó khăn đối những em học sinh. Mặc dù nhiên, những em học viên cần bắt buộc đọc kỹ đề và cẩn thận vận dụng và phối kết hợp được những kiến thức để giải quyết bài toán.Câu 3: Chiếm khoảng tầm 25% tổng điểm. Để có tác dụng được câu này, chúng ta học sinh cần có đầy đủ kỹ năng liên quan mang lại giải hệ phương trình, việc về con đường thẳng, đồ vật thị, hệ thức Vi-et. Câu hỏi sẽ với nhiều ý nhỏ theo thiết bị tự từ dễ cho khó nhằm mục đích phân hóa năng lực của thí sinh.Câu 4: Chiếm khoảng chừng 33% tổng điểm. Các kiến thức về hình học sẽ tập trung trong thắc mắc này. Bao gồm các phần nội dung tương quan đến chứng minh điểm, chứng minh tứ giác nội tiếp, tính góc, độ dài đoạn thẳng,… những ý càng về cuối càng bao gồm mức độ phân hóa cao hơn. Các bạn học sinh xem xét khi có tác dụng bàiCâu 5: Chiếm khoảng chừng 5% tổng điểm. Thắc mắc cuối đang cần học sinh tư duy những hơn, thay vững những kiến thức cơ bạn dạng là chưa đủ, bắt buộc vận dụng các kiến thức cải thiện để giải những dạng bài xích như minh chứng bất đẳng thức, tìm giá bán trị phệ nhất, nhỏ dại nhất,..Tuy nhiên thắc mắc này có mức giá trị điểm không cao nên các bạn thí sinh có thể lựa chọn làm hay là không dựa theo khả năng.Nắm trọn những dạng bài trong đề thi toán vào 10, tham khảo ngay:

Tổng quan liêu về loài kiến thức:
Phần Đại số:
Trong đề thi vào lớp 10 môn toán, phần đại số chiếm từ 6 đến 6,5 điểm. Trong đó, có tầm khoảng từ 5 – 6,5 điểm đến lựa chọn từ những kiến thức cơ bản hoặc các câu hỏi ở nút độ vận dụng thấp giúp các em học tập sinh rất có thể dễ dàng “ăn điểm” trọn vẹn trong trường hợp có tác dụng tỉ mỉ, chi tiết và cẩn thận.Lời khuyên trong phần Đại số này là các em học sinh cần ôn tập một giải pháp kĩ càng, hiểu thực chất của kỹ năng và kiến thức để rất có thể nắm trọn điện tuyệt đối hoàn hảo của phần này.Phần Hình học:
Phần hình học là phần những em học viên cần đặc biệt lưu ý. Bên cạnh việc nắm chắc các kiến thức về hình học, các em cũng cần được vẽ hình đúng chuẩn theo đúng yêu thương cầu câu hỏi vì giả dụ vẽ hình không thiết yếu xác, các em sẽ gặp gỡ phải rất nhiều khó khăn vào việc triển khai các yêu cầu mà đề bài xích ra.Tận dụng và khai thác triệt để toàn bộ các tính chất của những dạng hình theo dữ kiện nhưng mà đề bài xích đã ra với cách chứng minh của từng một số loại theo yêu thương cầu. Khi thực hiện trọn vẹn những điều này thì lúc gặp bất kể các bài tập hình học nào, các em học viên sẽ có khá nhiều ý tưởng và phương hướng xử lý bài toán.Trong những bài toán về Toán hình học thường trong đề thi vào 10 môn toán gồm từ 3 mang đến 4 ý cùng được phân chia theo từng cấp độ và độ nặng nề được thổi lên theo từng câu. Câu sau cuối phần lớn luôn là câu khó khăn nhất chỉ chiếm khoảng 0,5 điểm, còn các ý trên đa phần là số đông câu có giá trị 1 điểm.Chi ngày tiết về cấu tạo đề thi, những em học sinh có thể tham khảo bài xích viết: Cấu trúc đề thi vào 10 mới nhất
Bên cạnh đó, việc thực hành trực tiếp đề thi các năm là vấn đề rất đặc biệt để giúp các em học sinh hoàn toàn có thể hiểu rõ nhất cấu tạo và ma trận đề thi, từ bỏ đó đưa ra lộ trình và phương thức ôn thi cân xứng nhất dành cho bạn dạng thân. Các em học tập sinh rất có thể tham khảo trọn bộ tài liệu: Đề thi tuyển chọn sinh lớp 10 môn Toán được baivanmau.edu.vn xem tư vấn để thực hành thực tế và nhận xét hệ thống kiến thức mà các em đang ôn tập.









